数据结构-队列

　　昨天写了一篇关于数据结构栈的知识，今天有空就整理了一下队列。像栈一样，队列（queue）也是一种线性表，它的特性是先进先出，插入在一端，删除在另一端。把两者之间对比来看，可以发现各有优缺点吧！！！

一、队列的定义

1、队列是只允许在一端进行插入操作，而在另一端进行删除操作的线性表。队列有顺序队列和链队列，顺序队列在这里分成循环队列。

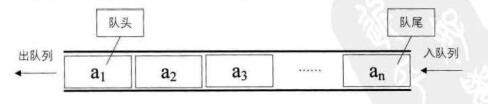
2、队列是一种先进先出的线性表，简称FIFO。允许插入的一端为队尾，允许删除的一端称为对头。如队列q=(a1,a2,.......,an)的示意图如下：

二、循环队列

1、队列顺序存储：假设队列有n个元素，则顺序存储的队列需要建立一个大于n的数组，并把队列的所有元素存储在数组的前n个单元，数组下标为0的一端即是对头；然后入队操作就是在队尾加一个元素，不需要移动任何元素，所以时间复杂度是O(1)；但是出队是在对头，即下标为0的位置，所以后面的所有元素得向前移动，以保证下标为0的位置不为空，时间复杂度为O(n)。

2、在1的情况下，如果不限制队列的元素必须存储在数组的前n个单元这一条件，则出队的性能就会大大增加，即对头不需要一定在下标为0的位置。如下图：

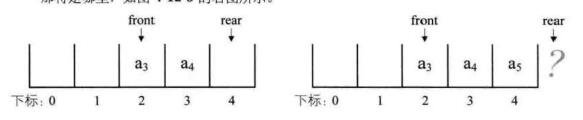
3、在2的情况下为了避免当只有一个元素时，对头和队尾重合使处理变麻烦，所以用front指针指向对头元素，rear指针指向队尾元素的下一个位置。当front等于rear时，就是空队列。如下图 ：

4、如下图所示，当入队a5时，rear指针都移动到数组之外去了，且如果接着入队的话，就会产生数组越界的错误，可实际上队列在下标为0和1的地方还是空闲的，把该种现象叫做“假溢出”。

5、循环队列定义：解决假溢出的办法就是后面满了，就再从头开始，也就是头尾想接的循环，把队列的这种头尾想接的顺序存储结构称为循环队列。

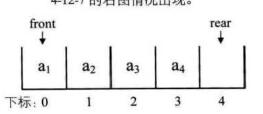
6、采用循环队列，如下图，此时font等于rear，是队列满时，但是在没采用循环队列的3的情况下，front等于rear是空队列的情况，此时采取的办法是当front=rear时依然是定义的空队列，而当数组中还有一个空闲空间时就定义是队列满时。如下图左边部分就认为是队列满，而不允许出现下图右边部分的情况。

7、采用6中定义队列满时，上图左边部分是一种满时情况，此时rear比front小，它们相差1，如下图也是一种满时情况，此时rear比front大，它们相差整整一圈。所以如果队列的最大尺寸为QueueSize，那么队列满的条件是(rear + 1) % QueueSize = front。

8、采用6中定义队列满时，如上图当rear大于front，此时队列的长度计算方式是：rear-front。如6中的图的左边部分所示，当rear小于front，此时队列长度分为两段，分别是QueueSize-front和0+rear，即rear-front+QueueSize，当图中rear不是指向1，而是指向0，这里的两段的计算方式也适合，所以通用的计算队列长度公式为：(rear - front + QueueSize) % QueueSize。

9、循环队列的顺序存储结构代码如下：

#define OK 1  
#define ERROR 0  
#define TRUE 1  
#define FALSE 0  
#define MAXSIZE 20 /* 存储空间初始分配量 */  
typedef int Status;   
typedef int QElemType; /* QElemType类型根据实际情况而定，这里假设为int */  
/* 循环队列的顺序存储结构 */  
typedef struct  
{  
    QElemType data[MAXSIZE];  
    int front;      /* 头指针 */  
    int rear;       /* 尾指针，若队列不空，指向队列尾元素的下一个位置 */  
}SqQueue;

10、循环队列的初始化代码：

/* 初始化一个空队列Q */  
Status InitQueue(SqQueue *Q)  
{  
    Q->front = 0;  
    Q->rear = 0;  
    return  OK;  
}

11、循环队列求队列长度代码：

/* 返回Q的元素个数，也就是队列的当前长度 */  
int QueueLength(SqQueue Q)  
{  
    return  (Q.rear - Q.front + MAXSIZE) % MAXSIZE;  
}

12、循环队列的入队列操作：

/* 若队列未满，则插入元素e为Q新的队尾元素 */  
Status EnQueue(SqQueue *Q, QElemType e)  
{  
    if ((Q->rear + 1) % MAXSIZE == Q->front)  /* 队列满的判断 */  
    {  
        return ERROR;  
    }     
    Q->data[Q->rear] = e;         /* 将元素e赋值给队尾 */  
    Q->rear=(Q->rear+1) % MAXSIZE;  /* rear指针向后移一位置， */  
                                    /* 若到最后则转到数组头部 */  
    return  OK;  
}

13、循环队列的出队列操作：

/* 若队列不空，则删除Q中队头元素，用e返回其值 */  
Status DeQueue(SqQueue *Q, QElemType *e)  
{  
    if (Q->front == Q->rear)          /* 队列空的判断 */  
    {  
        return ERROR;  
    }     
    *e = Q->data[Q->front];               /* 将队头元素赋值给e */  
    Q->front=(Q->front+1)%MAXSIZE;        /* front指针向后移一位置， */  
                                        /* 若到最后则转到数组头部 */  
    return  OK;  
}

三、队列的链式存储结构及实现

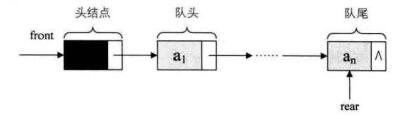
1、将队列的链式存储结构简称为链队列，为了操作方便，将对头指针指向链队列的头结点，而队尾指针指向终端结点，当front和rear都指向头结点时就是空队列，如下图：

2、链队列的结构代码：

#define OK 1  
#define ERROR 0  
#define TRUE 1  
#define FALSE 0  
#define MAXSIZE 20           /* 存储空间初始分配量 */  
typedef int Status;   
typedef int QElemType;       /* QElemType类型根据实际情况而定，这里假设为int */  
/* 结点结构 */  
struct QNode           
{  
   QElemType data;  
   struct QNode *next;  
};  
typedef struct QNode *QueuePtr;   
/* 队列的链表结构 */  
typedef struct            
{  
   QueuePtr front, rear;      /* 队头、队尾指针 */  
}LinkQueue;

3、入队操作：插入示意图如下：

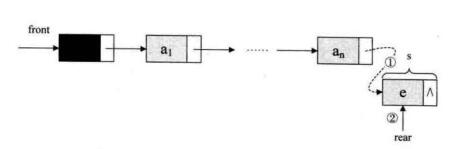
实现代码：

/* 插入元素e为Q的新的队尾元素 */  
Status EnQueue(LinkQueue *Q, QElemType e)  
{   
    QueuePtr s = (QueuePtr)malloc(sizeof(struct QNode));  
    if(!s) /* 存储分配失败 */  
    {  
        exit(OVERFLOW);  
    }     
    s->data = e;  
    s->next = NULL;  
    Q->rear->next = s;    /* 把拥有元素e的新结点s赋值给原队尾结点的后继，见图中① */  
    Q->rear = s;     /* 把当前的s设置为队尾结点，rear指向s，见图中② */  
    return OK;  
}

4、出队操作：出队操作时就是头结点的后继结点出队，将头结点的后继改为它后面的结点，若链表除头结点外只剩一个元素时，需要将rear指向头结点，如下图：

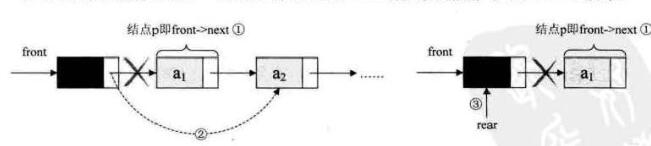
实现代码：

/* 若队列不空,删除Q的队头元素,用e返回其值,并返回OK,否则返回ERROR */  
Status DeQueue(LinkQueue *Q, QElemType *e)  
{  
    QueuePtr p;  
    if(Q->front == Q->rear)  
    {  
        return ERROR;  
    }     
    p = Q->front->next;             /* 将欲删除的队头结点暂存给p，见图中① */  
    *e = p->data;                  /* 将欲删除的队头结点的值赋值给e */  
    Q->front->next = p->next;     /* 将原队头结点的后继p->next赋值给头结点后继，见图中② */  
    if(Q->rear == p)           /* 若队头就是队尾，则删除后将rear指向头结点，见图中③ */  
    {  
        Q->rear = Q->front;  
    }     
    free(p);  
    return OK;  
}

四、总结回顾

　　在该篇博客中，我们学习了队列。结合上一篇知道了两者都是特殊的线性表，相当于对线性表也进行了一遍复习。接下来就总结一下两者的区别：

　　栈（Stack）是仅限在线性表表尾进行插入和删除操作的线性表。

　　队列（Queue）是只允许在一端进行插入操作，另一端进行删除操作的线性表。

　　它们都可以使用顺序存储结构来实现，但是会有一些弊端，不过也可以通过各自的技巧来解决，像两栈共享空间、循环队列。

　　当然它们也可以使用链式存储结构来实现。至于哪种实现更好，就取决于在实际使用中的场景了。

赏

谢谢你请我吃糖果