串可厉害了。不信?请看下面分解。
一、串的定义
1、串的定义:串(string)是由零个或多个字符组成的有限序列,又名叫字符串。一般记为s="a1a2.......an"(n>=0),其中s是串的名称,用双引号(有些书中是用单引号)括起来的字符序列是串的值,注意引号不属于串的内容。ai(1<=i<=n)可以是字母、数字或其他字符,i就是该字符在串中的位置。串中的字符数目n称为串的长度,定义中的“有限”指的是n是一个有限的数值。零个字符的串称为空串,它的长度为0,可以直接用两双引号表示,也可以用希腊字母“Φ”来表示。所谓的序列说明串的相邻字符之间具有前驱和后继的关系。
2、空格串:是只包含空格的串,注意与空串的区别,空格串是有内容有长度的,而且可以不止一个空格。
3、子串与主串:串中任意个数的连续字符组成的子序列称为该串的子串,相应地,包含子串的串称为主串。
4、子串在主串中的位置就是子串的第一个字符在主串中的序号。
5、串的逻辑结构与线性表类似,但是不同之处在于串中元素仅由一个字符组成。
二、串的比较
1、串在计算机中的大小取决于它们挨个字母的前后顺序,事实上,串的比较是通过组成串的字符之间的编码来进行的,而字符的编码指的是字符在对应字符集中的序号。
2、常用的字符是使用标准的ASCⅡ编码,是由7位二进制数表示一个字符,总共可以表示128个字符;后来扩展ASCⅡ码由8位二进制数表示一个字符,总共可以表示256个字符;后来有了Unicode编码,常用的是由16位的二进制数表示一个字符,总共可以表示约6.5万多个字符;为了和ASCⅡ码兼容,Unicode的前256个字符与ASCⅡ码完全相同。
3、两个串相等必须是它们串的长度以及它们各个对应位置的字符都相等时才算是相等。
2、判断两个串不相等的定义:给定两个串:s="a1a2......an",t="b1b2......bm",当满足以下条件之一时,s<t:
1)n<m,且ai=bi(i=1,2,......,n)。比如hap<happy。
2)存在某个k<=min(m, n),使得ai=bi(i=1,2,.......,k-1),ak<bk。比如s="happen",t="happy",两串的前4个字母都相同,而两串第5个字母(K值),字母e<y,所以s<t。
三、串的顺序存储结构
1、串的顺序存储结构是用一组地址连续的存储单元来存储串中的字符序列的。按照预定义的大小,为每个定义的串变量分配一个固定长度的存储区,一般是用定长数组来定义,所以存在一个预定义的最大串长度,一般可以将实际的串长度值保存在数组的0下标位置,也有的会定义存储在数组的最后一个下标位置,也有的会规定在串值后面加一个不计入串长度的结束标记字符,比如C语言的“\0”来表示串值的终结。如下图,此时要知道串的长度就需要遍历计算一下了。
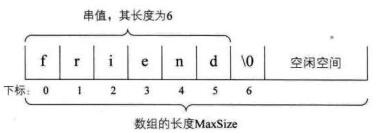
2、上面的串的顺序存储方式有点问题就是某些字符串的操作,比如新串的插入等操作都有可能使得串序列的长度超过了数组的长度MaxSize。所以对于串的顺序存储,串值的存储空间可在程序执行过程中动态分配而得。
四、串的链式存储结构
1、串的链式存储结构与线性表的链式存储结构类似,但是由于串的数据元素是一个字符,如果应用链表存储串值,一个结点对应一个字符就会造成很大的空间浪费,所以一个结点可以存放一个字符,也可以考虑存放多个字符,最后一个结点若是未被占满时,可以用“#”或其他非串值字符补全,如下图。

2、每个结点存放多少个字符才合适是很重要的,因为这直接影响着串处理的效率,应该根据实际情况做出选择。
3、串的链式存储结构除了在连接串与串操作时有一定的方便,总的来说不如顺序存储灵活,性能也没顺序存储好。
五、朴素的模式匹配算法
1、子串在主串中的定位操作通常称做串的模式匹配。
2、算法思路:对主串的每一个字符作为子串开头,与要匹配的字符串进行匹配。对主串做大循环,每个字符开头做T的长度的小循环,直到匹配成功或全部遍历完成位置。假设主串S和要匹配的子串T的长度存在S[0]和T[0]中,实现代码如下:
1 | /* 返回子串T在主串S中第pos个字符开始首次出现的位置。若不存在,则函数返回值为0。 */ |
3、时间复杂度分析:最好的情况是一开始就匹配成功,如“goodabc”中去匹配“good”,时间复杂度为O(1);稍差一些的情况是每次都是首字母就不匹配,则对T串的循环就必须进行了,如“abcdegood”中去匹配“good”,则时间复杂度为O(n+m),其中n为主串长度,m为要匹配的子串长度。根据等概率原则,所以这两种情况下的平均时间复杂度为O(n+m)。最坏的情况就是每次不成功的匹配都发生在串T的最后一个字符,在匹配时,每次都得将T中的字符循环到最后一位才发现根本不匹配,如下图:
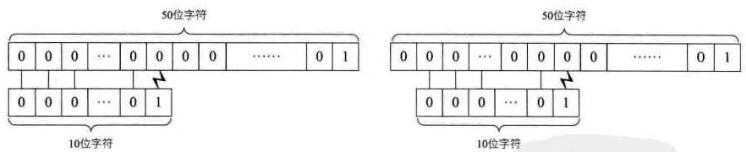
所以此时的时间复杂度为O((n-m+1)*m)。如下图:
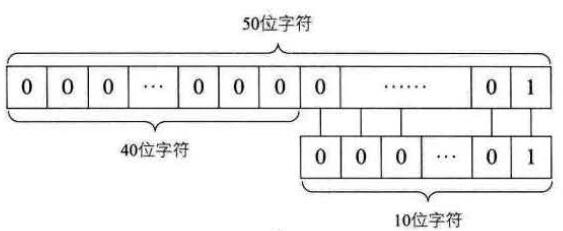
4、实际运算中,此算法太低效。
六、KMP模式匹配算法
KMP 模式匹配算法是由D.E.Knuth、J.H.Morris 和V.R.Pratt (其中 Knuth 和 Pratt 共同研究,Morris 独立研究)发表的一个模式匹配算法,可以大大避免重复遍历的情况,我们把它简称为克努特—莫里斯—普拉特算法,简称 KMP 算法。
1、KMP模式匹配算法原理:
KMP 算法的原理就在于省略那些不必要的判断。
举个例子,假如我们现在要匹配 P 串 “abcdeg”与 C 串“abcm”,后者是前者的子串。
在第一遍比对的时候,我们发现 P 串的前三位“abc”与 C 串的 “abc”是相等的,但是在第四位的时候却不相等了。
C 串的“adc” 这几个字母都没有重复,那么也就意味着,下次判断时,子串不用再往右移动一位再拿 “a” 和 P 串 “b” 进行比较,因为肯定是不相等的,直接跳到用 “a” 与 “d” 比较即可。
2、这里我和用到next数组值,(下面举几个例子就很容易理解了)
(1) T="abcdex"如下表所示:
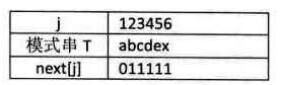
1)当j=1时,next[1]=0;
2)当j=2时,j由1到j一1就只有字符“a”,属于其他情况next[2]=1;
3)当j=3时,j由1到j—l串是”ab”,显然”a”与”b”不相等,属其他情况,next[3]=1;
4)以后同理,所以最终此T串的next[j]为011111。
(2)T="abcabx"(如下表所示)
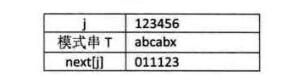
1) 当j=l时,next[l]=0;
2)当j=2时,同上例说明,next[2]=1,
3)当j=3时,同上,next[3]=1;
4)当j=4时,同上,next[4]=1;
5)当j=5时,此时j由1到j—l的串是”abca”,前缀字符”a”与后缀字符”a”相等,因此可推算出k值为2. 因此next[5]=2;
6)当j=6时,j由1到j一1的串是”ahcab”,由于前缀字符”ab”与后缀”ab”相等,所以next[6]=3。
我们可以根据经验得到如果前后缀一个字符相等,k值是2,两个字符k值是3,n个相等k值就是n+1.
3、KMP模式用算法实现,代码如下:

这段代码就是一个函数,目的是为了计算出当前要匹配的串T的next数组。主函数如下:

4、发现,KMP还是有缺陷的。比如,如果我们的主串S—"aaaabce",子串T="aaaaax",其next数组值分别为012345,在开始时,当,i=5、j=5时,我们发现‘b’与‘a’不相等,如下图(1),因此j=next[5]=4,如图中的(2),此时”b”与第4位置的‘a’依然不等,j=next[4]=3,如图中的(3),后依次是(4)(5),直到j=next[l]=0时,根据算法,此时i++,j++,得到i=6、j=l,如图中的(6)所示。
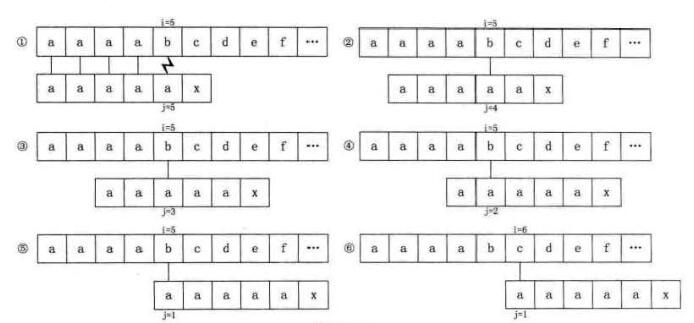
我们发现,当中的(2)(3)(4)(5)步骤,其实是多余的判断。由于T串的第二、三、四、五位置的字符都与首位的”a”相等,那么可以用首位nex[1]的值去取代与它相等的字符后续next[j]的值,这是个很好的办法。因此我们对求next函数进行了改良。
假设取代的数组为nextval,增加了加粗部分,代码如下:

5、这样改良版的nextval数值如下图几张表示:

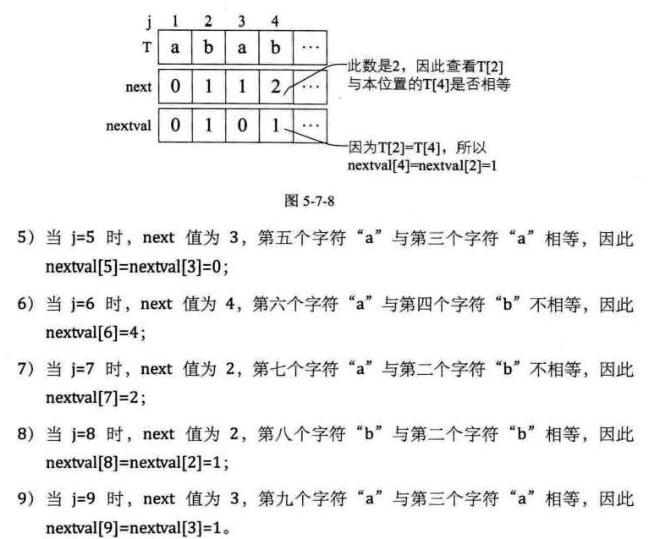
总结改进过的KMP算法,它是在计算出next值的同时,如果a位字符与它next值指向的b位字符相等,则该a位的nextval就指向b位的nextval值,如果不等.则该a位的nextval值就是它自己a位的next的值。
七、总结
这一篇我们重点讲了“串“这样的数据结构,串(string)是由零个或多个字符组成的有限序列,又名叫字符串。本质上,它是一种线性表的扩展。
但相对于线性表关注一个个元素来说,我们对串这种结构更多的是关注它子串的应用问题,如查找、替换等操作处现在的高级语言都有针对串的函数可以调用。我们在使用这些函数的时候,同时也应该要理解它当中的原理,以便于在碰到复杂的问題时,可以更加灵活的使用,比如KMP模式匹配算法的学习,就是更有效地去理解index函数当中的实现细节。多用心一点,说不定有一天,可以有以你的名字命名的算法流传于后世。
